Tomas PRO +4543
Jau kiek atslūgus emocijoms, kurias sukėlė šių metų matematikos valstybinis egzaminas, kviečiu jus atidžiau pažvelgti ir išsamiau išnagrinėti vieną iš šio egzamino užduočių. Štai apie ką kalbėsiu šioje temoje:
Uždavinio dalis 19.1. paženklinta raide B, kas reiškia, jog šiam uždaviniui išspręsti ypatingų žinių ar gabumų nereikia. Tiesa, šis uždavinys įvertintas tik 1 tašku, o tai taip pat reiškia, jog uždavinio sprendimas turėtų užimti vos keliasdešimt sekundžių.
Išties taip ir yra. Užtenka, jog egzamino metu prisimintum girdėjęs, kas yra aritmetinė progresija bei kokie skaičiai vadinami natūraliaisiais ir be jokių ypatingai gilių pamąstymų į galvą šautų pirmosios baigtinės aritmetinės progresijos tokios kaip: [tex]6;7;8[/tex] ar [tex]5;7;9[/tex] ir t.t. Suprantame, jog parašę nors vieną aritmetinę progresiją, tenkinančią duotą sąlygą, vienu šūviu nušauname du zuikius: t.y. atsakome į klausimą, o kartu ir pagrindžiame patį atsakymą. Tai ko gero vienas lengviausių uždavinių iš serijos: atsakyk į klausimą, o atsakymą pagrįsk.
Tad kodėl visgi nusprendžiau sukurti temą būtent šiam uždaviniui, nors buvo ir kur kas daugiau diskusijų sukėlusių uždavinių šiame, kaip patys abiturientai sako, net didžiausiems moksliukams sunkiai įveikiamame egzamine?
Viskas dėl to, jog šis uždavinys po kelių nedidelių pakeitimų sąlygos formuluotėje galėjo tapti iššūkiu net A lygiu gerai besimokiusiems mokiniams. Štai mano siūlomi variatai:
19.1. Ar skaičių suma gali būti lygi 1009? Atsakymą pagrįskite.
19.1. Ar skaičių suma gali būti lygi 1001? Atsakymą pagrįskite.
19.1. Ar skaičių suma gali būti lygi 437? Atsakymą pagrįskite.
Esminis faktorius, kuris skiria šiuos uždavinius nuo originalaus, yra tas, jog atsakymą pagrįsti tuo pačiu būdu, t.y. atrandu tinkamą atvejį ir jį parašau, užtruktų pernelyg ilgą laiką, o pirmojo mano pateikto uždavinio varianto atveju būtų lengva panirti į neviltį niekaip nerandant bent vienos tinkamos sekos. Aišku nesunku nustatyti šių uždavinių pasunkėjimo priežastį. Tai kur kas didesni nei originalioje sąlygoje duotas skaičiai. Tai mus jau verčia keisti mąstymo kryptį ir ieškoti tam tikra logika pagrįsto uždavinio sprendimo. Dabar pateiksiu šių uždavinių sprendimus. Todėl jei norite išmėginti savo jėgas, prieš skaitydami toliau pasistenkite įveikti užduotis patys.
Sprendimas:
Kol kas nagrinėkime apibendrintą atvejį ir tarkime, jog mūsų yra klausiama: ar skaičių suma gali būti lygi [tex]S[/tex]?
Turbūt nedaug minčių kyla, nuo ko reiktų pradėti gvildenti šią problemą. Bet tikiuosi daugeliui į galvą šauna mintis, jog reiktų pasinaudoti aritmetinės progresijos [tex]n[/tex] narių sumos formule. Ją turime dviem pavidalais: $$S_n=\dfrac{a_1+a_n}{2}\cdot n;\\S_n=\dfrac{2a_1+(n-1)d}{2}\cdot n$$ Toliau ko gero akivaizdu, jog pasirinkę bet kurią lygybę vietoje [tex]S_n[/tex] galėtume įsistatyti sąlygoje minimą skaičių, t.y. 1009, 1001 ar 437 priklausomai nuo to, kurį uždavinį sprendžiame, bet kaip jau nutarėm dabar spręsime uždavinį be konkrečių reikšmių. Taigi rašome [tex]S_n=S[/tex]:
Pernelyg nesvarstydami pasirinkime pirmąją lygybę (tiesiog paprasčiau atrodo). Tada iš jos galime užrašyti štai ką: $$a_1+a_n=\dfrac{2S}{n}$$ Gal nujaučiate, kam mes taip padarėme? Jei ne, tai siūlyčiau pagalvoti, kokiai skaičiui aibei turi priklausyti dydžio [tex]a_1+a_n[/tex] reikšmė. Tikiu, jog ilgai nedvejodami galite pasakyti, jog natūraliųjų, kadangi iš sąlygos žinoma, jog aritmetinės progresijos nariai yra natūralieji skaičiai. Toliau jau taip ko gero aišku, jog esant lygybei tarp dydžių [tex]a_1+a_n[/tex] ir [tex]\dfrac{2S}{n}[/tex] mes turime pareikalauti, jog ir [tex]\dfrac{2S}{n}[/tex] reikšmė būtų natūralusis skaičius. Šitaip galime suformuluoti būtinąją, bet nepakankamą sąlygą, jog [tex]n[/tex] sekos [tex]a_n[/tex] narių, kurių suma [tex]S[/tex], sudarytų aritmetinę progresiją.
Būtina, bet nepakankama sąlyga, jog egzistuotų baigtinė aritmetinė progresija [tex]a_n[/tex] ([tex]n>2[/tex]), kurios visi [tex]n[/tex] nariai - natūralieji skaičiai, o jų suma [tex]S_n=S[/tex]:$$\dfrac{2S}{n}∈ \mathbb{N}$$[tex]\bullet[/tex] Vadinasi, jei su tam tikromis [tex]n[/tex] ir [tex]S[/tex] reikšmėmis [tex]\dfrac{2S}{n}∈ \mathbb{N}[/tex] bus klaidingas teiginys, tai reikš, jog neegzistuoja tokia aritmetinė progresija, kurios visi [tex]n[/tex] nariai yra natūralieji skaičiai, o jų suma lygi [tex]S[/tex].
[tex]\bullet[/tex] Bet jei su tam tikromis [tex]n[/tex] ir [tex]S[/tex] reikšmėmis [tex]\dfrac{2S}{n}∈ \mathbb{N}[/tex] bus teisingas teiginys, tai reikš, jog galbūt egzistuoja tokia aritmetinė progresija, kurios visi [tex]n[/tex] nariai yra natūralieji skaičiai, o jų suma lygi [tex]S[/tex], bet tam nustatyti reikalingas papildomas tyrimas.
[tex]\rhd[/tex] Dabar galime pamėginti atsakyti į klausimą: ar skaičių suma gali būti lygi 1009?
Turime [tex]S_n=1009[/tex], vadinasi: [tex]\dfrac{2S_n}{n}=\dfrac{2\cdot 1009}{n}[/tex]
Kadangi 2 ir 1009 yra pirminiai skaičiai, tai [tex]2\cdot 1009[/tex] dalijasi iš šių skaičių:
[tex]1;\space 2;\space 1009;\space 2\cdot 1009.[/tex] Tai yra galimos [tex]n[/tex] reikšmės. Prisimename, jog rastos natūraliosios [tex]n[/tex] reikšmės negarantuoja, jog aritmetinė progresija, turinti [tex]n[/tex] natūraliųjų narių, kurių suma lygi [tex]1009[/tex], egzistuoja. Taigi turime patikrinti šias reikšmes: pirmąsias dvi reikšmes atmetame, nes [tex]n>2[/tex]. Atmeskime ir paskutines dvi reikšmes, kadangi neegzistuoja tokia didėjančioji aritmetinė progresija, kurios narių kiekis būtų lygus ar didesnis už jų sumą, t.y. [tex]n≥S_n[/tex], o sekos nariai - natūralieji skaičiai.
Atsakome į uždavinio klausimą: Negali būti.
[tex]\rhd[/tex] Toliau nagrinėkime atvejį, kai: [tex]S_n=1001[/tex]
Tada [tex]2S_n[/tex] atitinkamai lygu: [tex]2002[/tex]
Šį skaičių išskaidę pirminiais dauginamaisiais, gauname:
[tex]2002=2\cdot 7\cdot 11\cdot 13[/tex];
Skaičiaus [tex]2002[/tex] dalikliai didesni už 2: 7, 11, 13, 14, 22, 26, 77, 91, 143, 154, 182, 286, 1001, 2002.
Vėlei ne visos [tex]n[/tex] reikšmės mums tinkamos, tačiau mums užtenka rasti bent vieną [tex]n[/tex] reikšmę, jog skaičiai [tex]a_i∈ \mathbb{N}[/tex], kai [tex]i=\overline{1..n}[/tex], sudarytų didėjančią aritmetinę progresiją, kurių suma [tex]1001[/tex].
Imkime [tex]n=7[/tex].
Tuomet pasinaudoję antrąja aritmetinės progresijos narių sumos formule, galime užrašyti:
$$1001=\dfrac{2a_1+(7-1)d}{2}\cdot 7$$ Sutvarkę, gauname: $$a_1+3d=143$$ Gauname diofantinę lygtį, t.y. lygtį pavidalu: [tex]ax+by=c[/tex], kur [tex]a, b, c[/tex] koeficientai, kurių reikšmės sveikieji skaičiai, o lygties sprendiniai yra sveikųjų skaičių [tex]x[/tex] ir [tex]y[/tex] poros: [tex](x;y)[/tex]. Diofantinės lygtys paprastai turi be galo daug sprendinių, tačiau šiuo atveju mums pakaks rasti nors vieną sprendinį. Be to atsižvelgiant į tai, jog šį ir sekančius uždavinius spręsime ieškodami natūraliųjų skaičių porų, verta paminėti, jog tokiu atveju sprendinių aibė yra baigtinė.
Pastebėkime, jog jei mums pavyks rasti sąlygą tenkinančią aritmetinę progresiją, tai iškart galime nurodyti, jog jos ketvirtas narys bus lygus 143, nes pagal bendrojo nario formulę: [tex]a_4=a_1+3d[/tex].
Imkime [tex]d=1[/tex], tada: [tex]a_1=143-3d=143-3=140[/tex].
Kai turime [tex]n,\space a_1,\space d[/tex] reikšmes [tex](7;\space 140;\space 1)[/tex], mes nusakome baigtinę didėjančią aritmetinę progresiją, sudarytą iš natūraliąsias reikšmes įgyjančių narių.
Šiuo atveju ji yra: [tex]140;\space 141;\space 142\space 143;\space 144;\space 145;\space 146.[/tex]
Atsakome į uždavinio klausimą: Gali būti.
[tex]\rhd[/tex] Atvejį, kai: [tex]S_n=437[/tex] panagrinėkite patys. Ši suma galima, pamėginkite tai įrodyti.
Grįžkime prie originalios uždavinio sąlygos. Kaip jau rašiau anksčiau nustatyti, jog skaičių suma 21 yra galima, lengva be didelių skaičiavimų ar atrankų. Tačiau kas jei uždavinio sąlyga skambėtų taip:
19.1. Raskite visas progresijas, kurių narių suma lygi 21.Ar esate tikri, jog išrašytumėte visus galimus atvejus? Pamėginkime išspręsti šią užduotį.
Sprendimas:
Nustatome reikšmes kandidates, kurias gali įgyti dydis [tex]n[/tex]:
[tex]\dfrac{2S_n}{n}∈ \mathbb{N}\implies \dfrac{2\cdot 21}{n}=\dfrac{2\cdot 3\cdot 7}{n}∈ \mathbb{N}[/tex]
[tex]n>2:\space n∈\{3;\space 6;\space 7;\space 14;\space 21;\space 42\}[/tex]
Su kiekviena iš šių reikšmių sudarome diofantinę lygtį:
[tex]\bullet[/tex] Kai [tex]n=3:[/tex] $$\dfrac{2a_1+(n-1)d}{2}\cdot n=S_n\implies \dfrac{2a_1+(3-1)d}{2}\cdot 3=21\implies a_1+d=7$$ Nesunkiai nustatome visas galimas sprendinių poras [tex](a_1;d)[/tex]: [tex](1;6),\space (2;5),\space (3;4),\space(4;3),\space(5;2),\space(6;1);[/tex]
Galime užrašyti ir pačias aritmetines progresijas:
[tex](1;\space 7;\space 13),\space (2;\space 7;\space 12),\space(3;\space 7;\space 11),\space(4;\space 7;\space 10),\space(5;\space 7;\space 9),\space(6;\space 7;\space 8).[/tex]
[tex]\bullet[/tex] Kai [tex]n=6:[/tex] $$\dfrac{2a_1+(n-1)d}{2}\cdot n=S_n\implies \dfrac{2a_1+(6-1)d}{2}\cdot 6=21\implies 2a_1+5d=7$$ Nesunkiai nustatome vienintelę galimą sprendinių porą: [tex](a_1;d)[/tex]: [tex](1;1);[/tex]
Užrašome dar vieną progresiją: [tex](1;\space 2;\space 3;\space 4;\space 5;\space 6)[/tex].
Akivaizdu, jog lygtys, kurias gauname su likusiomis [tex]n[/tex] reikšmėmis natūraliųjų sprendinių porų neturi, t.y. lygtys: $$2a_1+6d=6;\\2a_1+13d=3;\\2a_1+20d=2;\\2a_1+41d=1;$$ Taigi viso gauname 7 didėjančias aritmetines progresijas, sudarytas iš natūraliąsias reikšmes įgyjančių narių, kurių suma lygi 21:
[tex](1;\space 7;\space 13),\space (2;\space 7;\space 12),\space(3;\space 7;\space 11),\space(4;\space 7;\space 10),\space(5;\space 7;\space 9),\space(6;\space 7;\space 8),\space(1;\space 2;\space 3;\space 4;\space 5;\space 6).[/tex]
Nepamirškime ir antrosios 19 uždavinio dalies. Sąlyga atrodo taip:
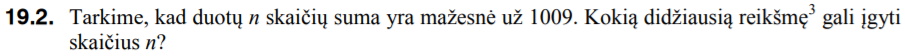
Kol kas vienintelis matytas šio uždavinio sprendimas rėmėsi tokiu samprotavimu, kad daugiausiai pavyks sudėti aritmetinės progresijos narių, kurių suma mažesnė už tam tikrą skaičių, tuomet, kai pirmasis narys ir progresijos skirtumas bus kiek galima mažiausi, t.y. lygūs 1.
Tuomet remdamiesi aritmetinės progresijos narių sumos formule sudarome nelygybę:$$\dfrac{2\cdot 1+(n-1)\cdot 1}{2}\cdot n<1009$$Ją išsprendžiame ir randame didžiausią natūralų sprendinį. Šiuo atveju jis lygus [tex]n=44[/tex].
Kaip galima mėginti spręsti šį uždavinį kitaip? Pasinaudokime lygybe, gaunama iš aritmetinės progresijos narių sumos formulės: $$2a_1+(n-1)d=\dfrac{2S_n}{n}$$Žinome, kad [tex]S_n<1009[/tex], t.y.: [tex]2S_n<2018[/tex]. Vadinasi mūsų tikslas yra rasti tokį [tex]2S_n[/tex], kuris būtų mažesnis už 2018, bet turėtų kiek galima didžiausią daliklį [tex]n[/tex], nes [tex]\dfrac{2S_n}{n}∈ \mathbb{N}[/tex], kuris tenkina lygties:$$2a_1+(n-1)d=\dfrac{2S_n}{n}$$natūraliųjų sprendinių poros ar porų [tex](a_1;d)[/tex] būtinąją, bet nepakankamą egzistavimo sąlygą, kuri yra tokia: $$n-1<\dfrac{2S_n}{n}$$ arba:$$n(n-1)<2S_n$$ Kadangi [tex]2S_n<2018[/tex], tai: $$n(n-1)<2018$$ Nesunkiai nustatome (iš skaičiaus 2018 ištraukę kvadratinę šaknį) šios nelygybės didžiausią natūralų sprendinį, kai skaičiui 2018 artimiausias natūralaus skaičiaus kvadratas yra: [tex]45^2[/tex] (aišku galima ir spręsti šią nelygybę). Patikrinę, gauname: kai [tex]n=45[/tex], tai: $$n(n-1)=45\cdot 44=1980<2018$$ Kadangi: [tex]2S_n<2018[/tex], tai imame vienetu mažesnę [tex]n[/tex] reikšmę [tex](44)[/tex], o vietoje [tex]2S_n[/tex] rašome 1980. Tada bus tenkinama nelygybė: $$n(n-1)<2S_n$$, t.y. $$44\cdot 43<1980=45\cdot 44$$ bei sąlyga: $$\dfrac{2S_n}{n}=\dfrac{1980}{44}=45∈ \mathbb{N}.$$ Gauname, jog didžiausia galima [tex]n[/tex] reikšmė galėtų būti [tex]44[/tex]. Patikrinkime, jog ši reikšmė ir yra uždavinio atsakymas: $$2a_1+(n-1)d=\dfrac{2S_n}{n}\implies2a_1+43d=45\implies a_1=1,\space d=1$$
Tai patvirtina, jog uždavinio atsakymas: [tex]44[/tex].
Įdomu tai, jog spręsdami šį uždavinį šiuo būdu mes įrodome du dalykus: pirma, jog daugiausiai galima sudėti 44 narius ir taip pat, jog [tex]a_1=d=1[/tex], kur pastarąją sąlygą pirmuoju sprendimo būdu priėmėme be griežto pagrindimo.
Užduotys jums:
Kiek yra tokių didėjančių aritmetinių progresijų [tex]a_n\space(n>2)[/tex], kurių nariai yra natūralieji skaičiai, o jų suma lygi 126?
Patvirtinkite arba paneikite teiginį: Negalima sudaryti didėjančios aritmetinės progresijos [tex]a_n[/tex] [tex](n>2)[/tex], kurios nariai yra natūralieji skaičiai, o jų suma - pirminis skaičius.
Kiek daugiausiai didėjančios aritmetinės progresijos narių, kurie visi yra natūralieji skaičiai, galima sudėti, jog suma būtų mažesnė už 853? Išspręskite dviem būdais, pateiktais šioje temoje, ir patikrinkite, ar atsakymai sutampa.

