Tomas PRO +4543
Pagal klasikinį tikimybės apibrėžimą įvykio A tikimybė lygi:
[tex]P(A)=\dfrac{m}{n}[/tex], kur [tex]m[/tex]-įvykiui A palankių baigčių skaičius, [tex]n[/tex]-visų įvykių, galinčių įvykti atliekant bandymą, skaičius.
Tačiau ne visas tikimybes galime apskaičiuoti taip. Kartais atsitinka taip, kai bandymo baigčių skaičius yra "nesuskaičiuojamas". Štai jums pavyzdys:
Į skritulį, įbrėžtas kvadratas. Įvykis A-"atsitiktinai parinktas skritulio taškas priklauso kvadratui"
Nustatyti, kokie elementarieji įvykiai sudaro bandymą ir kurie jų priklauso įvykiui A nesunku. Visas bandymo baigtis sudaro visi skrituliui priklausantys taškai, o įvykį A sudaro tie skritulio taškai, kurie priklauso kvadratui". Tačiau, kai ateina laikas suskaičiuoti kiek tų taškų yra prasideda problemos. Jų suskaičiuoti neįmanoma!
Čia į pagalba ateina geometrinės tikimybės apibrėžimas.
Jei bandymo baigčių ir įvykiui A palankių baigčių sričių dydžiai išmatuojami tam tikrais matais (ilgio, ploto, tūrio...), o tikimybė patekti į bet kurią srities dalį yra proporcinga tos dalies matui, tai įvykio A tikimybė lygi:
[tex]P(A)=\dfrac{|q|}{|Q|}[/tex], kur [tex]|Q|[/tex]([tex]|q|[/tex])-bandymo (įvykiui A palankių) baigčių srities dydis tam tikrais matais.
Tiesa [tex]q⊆Q[/tex], tai reiškia, jog visi sričiai [tex]q[/tex] priklausantys taškai turi priklausyti ir sričiai [tex]Q[/tex]
Vadinasi bandymo su skrituliu ir kvadratu atveju turime, kad:
[tex]|Q|-[/tex]skritulio plotas.
[tex]|q|-[/tex]kvadrato plotas.
Tada: [tex]P(A)=\dfrac{|q|}{|Q|}[/tex]
Paskaičiuokime šią tikimybę:
Tarkime skritulio spindulys: [tex]R[/tex], tada įbrėžto kvadrato kraštinė lygi: [tex]a=\sqrt{R^2+R^2}=R\sqrt{2}[/tex]
Tuomet skritulio plotas lygus: [tex]|Q|=πR^2[/tex]
Kvadrato plotas lygus: [tex]|q|=a^2=2R^2[/tex]
Vadinasi:
[tex]P(A)=\dfrac{|q|}{|Q|}=\dfrac{2R^2}{πR^2}=\dfrac{2}{π}[/tex]
Tarkime į išpjautą skritulį, kuriame įbrėžtas kvadratas, metame strėlytes. Tai darome pakankamai daug kartų ([tex]n[/tex]) ir suskaičiuojame, kiek kartų strėlytės pataikė į kvadrato ribojamą plotą ([tex]k[/tex]). Tuomet santykis pataikymo į kvadrato ribojamą plotą dažnis [tex]\dfrac{k}{n}[/tex] artėtų prie apskaičiuotos tikimybės [tex]P(A)[/tex].
Tada sudarę lygtį: [tex]\dfrac{k}{n}≈\dfrac{2}{π}[/tex] gautume, jog apytikslę [tex]π[/tex] reikšmę galime paskaičiuoti taip: [tex]π≈\dfrac{2n}{k}[/tex]
Galėtume sakyti, jog geometrinės tikimybės pritaikymo atvejai aiškūs, tačiau ne visada jie tokie akivaizdūs. Geometrinės tikimybės apibrėžime buvo minima, jog bandymo baigtims priklausanti sritis gali būti matuojama įvairiais matavimo vienetais. Tačiau ką daryti, jei ta sritis yra matuojama tarkime laiko vienetais? Kaip tokiu atveju pritaikyti geometrinės tikimybės skaičiavimo formulę? Štai užduotis:
Du draugai susitarė susitikti tarp 12 ir 13 valandos. Jie nutarė, kad pirmas atėjęs palauks antrojo 15 minučių, o jei šis nepasirodys, išeis iš sutartos vietos. Tarp 12 ir 13 valandos draugai ateina atsitiktinai. Kokia tikimybė, kad jie susitiks?
Taikydami klasikinį tikimybės apibrėžimą šio uždavinio tikrai neišspręsime, nes ir vėl turime be galo daug elementariųjų įvykių (draugų pasirodymų laikų), kurių suskaičiuoti negalime. Taigi privalome taikyti geometrinės tikimybės skaičiavimo taisyklę. Tačiau čia ir vėl iškyla klausimas, kaip paskaičiuoti sričių [tex]Q[/tex] ir [tex]q[/tex] dydžius. Pamėginkime nusibrėžti koordinačių sistemą. Horizontalioje ašyje esantys taškai žymės visus galimus laiko momentus, kai į sutartą vietą ateina pirmasis draugas, o vertikalioje ašyje - laiko momentus, kai ateina antrasis. Laiką matuokime valandomis, o pradinį laiko momentą laikykime 0.
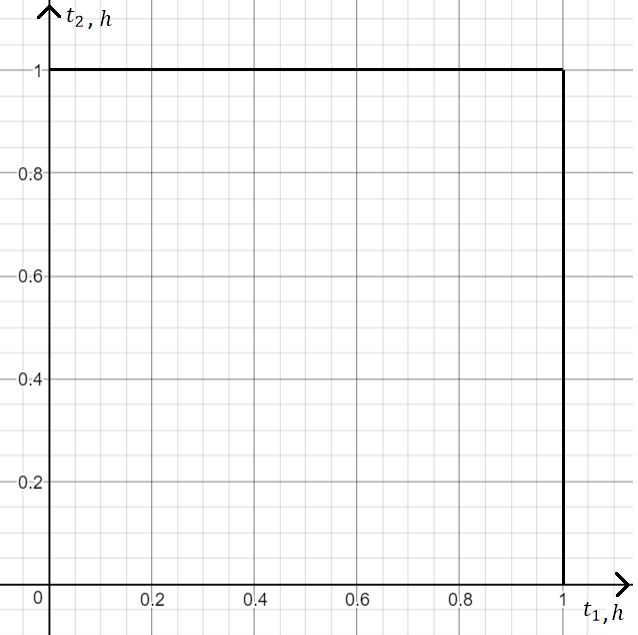
Tada srities (kurią pažymėjau kvadratu) taškai žymi visus galimus draugų atvykimo į vietą momentus, pavyzdžiui taškas (0,5;0,75) reikštų, jog pirmasis į vietą atvyko 12h30 min, o antrasis 12h 45 min. Vadinasi akivaizdu, jog visų galimų baigčių srities dydis lygus kvadrato 1X1 plotui: [tex]|Q|=1\cdot 1=1[/tex].
Nustatykime srities [tex]q[/tex] dydį:
Pagal sąlygą draugų atvykimo laiko skirtumas negali būti didesnis už 15 min, t.y. 1/4 valandos, vadinasi galime užrašyti, kad:
[tex]|t_1-t_2|≤\dfrac{1}{4}[/tex]
Vadinasi sričiai [tex]q[/tex] priklauso taškai [tex](t_1;t_2)∈Q[/tex], kurie tenkina nelygybę: [tex]|t_1-t_2|≤\dfrac{1}{4}[/tex].
Pervarkome nelygybę:
[tex]|t_1-t_2|≤\dfrac{1}{4}\implies \begin{cases} t_1-t_2≤\dfrac{1}{4} \\ t_1-t_2≥-\dfrac{1}{4} \end{cases}\implies \begin{cases} t_2≥t_1-\dfrac{1}{4} \\ t_2≤t_1+\dfrac{1}{4} \end{cases}[/tex]
Nubrėžiame tieses [tex]t_2(t_1)=t_1-\dfrac{1}{4}[/tex] ir [tex]t_2(t_1)=t_1+\dfrac{1}{4}[/tex]. Pažymime tą bendrą sritį, kurios taškai yra aukščiau pirmos tiesės, bet žemiau antros tiesės.
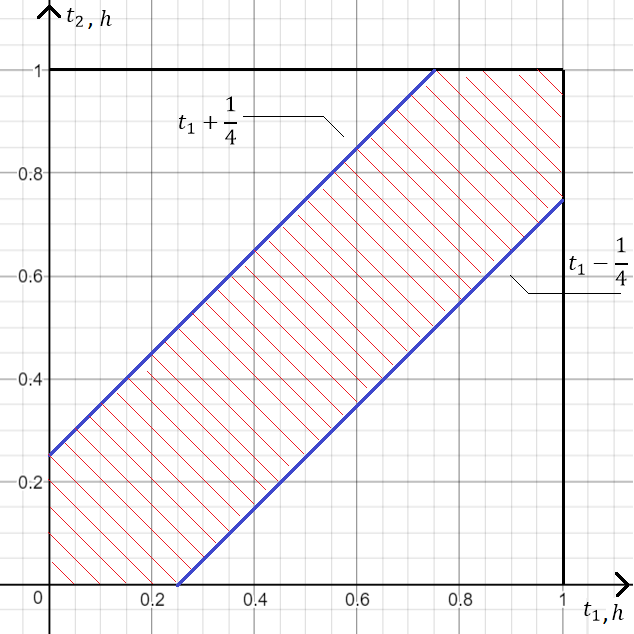
Šios srities dydis lygus [tex]|q|[/tex]. Liko jį paskaičiuoti.
[tex]|q|=1-(\dfrac{1}{2}\cdot \dfrac{3}{4}\cdot \dfrac{3}{4}+\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot \dfrac{3}{4})=1-\dfrac{18}{32}=\dfrac{14}{32}=\dfrac{7}{16}[/tex]
Kai [tex]A[/tex]-"draugai susitiko", tai:
[tex]P(A)=\dfrac{|q|}{|Q|}=\dfrac{\frac{7}{16}}{1}=\dfrac{7}{16}[/tex]
Panagrinėkime paskutinį pavyzdį:
Kvadratinės lygties [tex]x^2+px+q=0[/tex] koeficientai parenkami iš intervalo (0;1). Kokia tikimybė, kad lygtis turės realius sprendinius?
Šis uždavinys būtų išsprendžiamas klasikinio tikimybės skaičiavimo būdu, jei būtų duotas kiek didesnis intervalas, o koeficientų reikšmės galėtų būti tik sveikieji skaičiai, tada bandymo baigtys būtų suskaičiuojamos. Tačiau dabar turėsime taikyti geometrinės tikimybės skaičiavimo formulę.
Taigi uždavinį sprendžiame taip:
Kvadratinė lygtis turi realių sprendinių, kai [tex]D≥0[/tex]. [tex]D=p^2-4q≥0\implies p^2≥4q\implies q≤\dfrac{p^2}{4}[/tex]. Koordinačių plokštumoje nubrėžiame kvadratinės funkcijos [tex]q(p)=\dfrac{p^2}{4}[/tex] grafiką.

Kadangi [tex]q,p∈(0;1)[/tex], tai srities [tex]Q[/tex] dydis lygus kvadrato 1X1 plotui. Sričiai [tex]q[/tex] priklauso visi taškai [tex](q;p)∈Q[/tex], kurie tenkina sąlygą: [tex]q≤\dfrac{p^2}{4}[/tex]. Ši sritis pažymėta raudonai.
Vadinasi: [tex]|Q|=1\cdot 1=1[/tex]
[tex]|q|=\int\limits_{0}^{1}{\dfrac{1}{4}p^2}dp=\dfrac{p^3}{12}|_{0}^1=\dfrac{1}{12}[/tex]
Kai įvykis [tex]A-[/tex]"sudaryta kvadratinė lygtis turi realių sprendinių", tai:
[tex]P(A)=\dfrac{|q|}{|Q|}=\dfrac{\frac{1}{12}}{1}=\dfrac{1}{12}[/tex]
pakeista prieš 7 m