Logaritmines nelygybės sprendimas

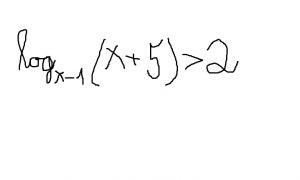
Kaip išspręsti šią logaritminę nelygybę?

MilkhaterTaikyk pagrindo keitimo formulę

kadangi logaritmo pagrindas (x-1) gali būt tiek didesnis už 1 tiek mažesnis reikia nagrinėt du atvejus. Dvi sistemas.

1)
[tex]\[\left\{ \begin{array}{l}
x - 1 > 1\\
x + 5 > 0\\
x + 5 > {(x - 1)^2}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
x > 2\\
x >  - 5\\
{x^2} - 3x - 4 < 0
\end{array} \right. \Rightarrow \][/tex][tex]\[\left\{ \begin{array}{l}
x > 2\\
(x + 1)(x - 4) < 0
\end{array} \right.\][/tex]
pirmos sistemos sprendinių aibė yra x∈(2;4)

2)
[tex]\[\left\{ \begin{array}{l}
0 < x - 1 < 1\\
x + 5 > 0\\
x + 5 < {(x - 1)^2}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
1 < x < 2\\
x >  - 5\\
{x^2} - 3x - 4 > 0
\end{array} \right.\][/tex][tex]\[ \Rightarrow \left\{ \begin{array}{l}
x > 2\\
(x + 1)(x - 4) > 0
\end{array} \right.\][/tex]
antra sistema sprend. neturi.

taigi Atsakymas kai x∈(2;4)

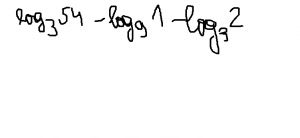
Kartojuosi senas temas, neprisimenu visiškai logaritmų, todėl norėjau paklausti, kaip keičiami logaritmo pagrindai?:)

su pagrindo keitimo formule.

bet tau užteks šitos, 9 perašyk kaip 3, o 2 iškelt į priekį po vienetu pakišus. (1/2)

toliau 1/2 perkelt ant pologortiminio skaičiaus...


gausi [tex]log_3(54)-log_3(1)-log_3(2)[/tex]
taikysi formule:

[tex]log_3(54/2)=log_3(27)=log_3(3^3)=3log_3(3)=3*1=3[/tex]