Nykstamosios funkcijos. Ekvivalenčių nykstamųjų funkcijų taikymas skaičiuojant ribas

Ankstesnėse pamokose mes jau išnagrinėjome visus dažniausiai pasitaikančius neapibrėžtumus skaičiuojant ribas. Šią temą skirsiu nykstamųjų funkcijų nagrinėjimui, sužinosime jų savybes, bei aptarsime, ką vadiname ekvivalenčiomis nykstamosiomis funkcijomis ir išmoksime jas taikyti skaičiuojant ribas. Su nykstamosiomis funkcijomis pažintį pradėkime nuo tokio apibrėžimo:

Funkcija [tex]\alpha(x)[/tex] vadinama nykstamąja, kai [tex]x\to a[/tex] (arba kai [tex]x\to \infty[/tex]), jeigu jos riba lygi nuliui.

Tai ko gero, vienas iš paprastesnių apibrėžimų. Remiantis juo galime galime sakyti, jog funkcija [tex]f(x)=x-1[/tex] yra nykstamoji, kai [tex]x\to 1[/tex], kadangi:$$\lim\limits_{x\to1}(x-1)=0.$$ Arba funkcija [tex]f(x)=\dfrac{1}{x}[/tex] yra nykstamoji, kai [tex]x\to \infty[/tex], kadangi:$$\lim\limits_{x\to\infty}\dfrac{1}{x}=0.$$ Kalbant apie vieną iš nykstamųjų funkcijų savybių yra reikalinga aprėžtosios funkcijos sąvoka:

Funkcija [tex]f(x)[/tex] yra aprėžta tam tikrame intervale, jeigu egzistuoja toks skaičius [tex]M>0[/tex], kad su visomis [tex]x[/tex] reikšmėmis iš duoto intervalo teisinga nelygybė [tex]|f(x)|≤M[/tex].

Pavyzdžiui funkcija [tex]\sin x[/tex] yra aprėžta visoje savo apibrėžimo srityje (žiūrėti paveikslėlį žemiau), nes kai [tex]M=1[/tex], tai [tex]∀x∈(-\infty;\infty)[/tex], gauname, kad [tex]|\sin x|≤1[/tex].

Galimas ir kitas aprėžtosios funkcijos apibrėžimas:

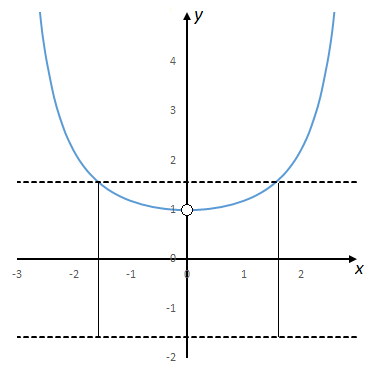
Funkcija [tex]f(x)[/tex] vadinama aprėžta, kai [tex]x\to a[/tex], jei egzistuoja tokie dydžiai [tex]\delta,M>0[/tex], kad su visais [tex]x[/tex], su kuriais teisinga nelygybė [tex]|x-a|<\delta[/tex], teisinga ir nelygybė [tex]|f(x)|≤M.[/tex]

Pavyzdžiui funkcija [tex]f(x)=\dfrac{x}{\sin x}[/tex] yra aprėžta, kai [tex]x\to 0[/tex] (paveikslėlis žemiau), nes kai [tex]M=\delta=\dfrac{\pi}{2}[/tex], tai su visais [tex]x∈\left(-\dfrac{\pi}{2};\dfrac{\pi}{2}\right)\backslash\{0\}[/tex] yra teisinga nelygybė [tex]\left|\dfrac{x}{\sin x}\right|≤\dfrac{\pi}{2}[/tex]

Aprėžtosios funkcijos apibrėžimas galimas ir kai argumentas artėja į begalybę:

Funkcija [tex]f(x)[/tex] vadinama aprėžta, kai [tex]x\to\infty[/tex], jei egzistuoja tokie skaičiai [tex]M,N>0[/tex], jog su visomis [tex]x[/tex] reikšmėmis, kurios tenkina nelygybę [tex]|x|>N[/tex] yra teisinga nelygybė [tex]|f(x)|≤M[/tex].

Pastaba: Funkcija taip pat gali būti aprėžta ir tik kažkuriuo vienu iš atvejų, t.y. kai [tex]x\to-\infty[/tex] arba [tex]x\to+\infty[/tex], apibrėžimą galime naudoti tą patį, tik [tex]|x|>N[/tex] pirmuoju atveju keičiame į [tex]x<-N[/tex], o antruoju į [tex]x>N[/tex].

Pavyzdžiui funkcija [tex]y=\sin x[/tex] (pirmas paveikslėlis) yra aprėžta, kai [tex]x\to \infty[/tex], nes pasirinkę bet kurį [tex]N>0[/tex], gauname, kad su visais [tex]x[/tex], tenkinančiais sąlygą [tex]|x|>N[/tex] yra teisinga nelygybė [tex]|\sin x|≤1[/tex].
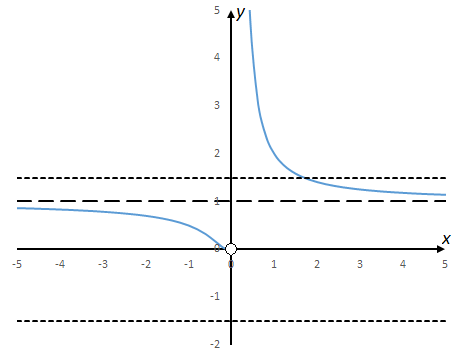
Kitas pavyzdys būtų funkcija [tex]f(x)=2^{\frac{1}{x}}[/tex] (paveikslėlis žemiau). Ši funkcija yra aprėžta kai [tex]x\to-\infty[/tex], nes pasirinkę [tex]M=1,5[/tex] ir [tex]N=1[/tex], gauname, jog su visomis [tex]x<-1[/tex] reikšmėmis yra teisinga nelygybė [tex]\left|2^{\frac{1}{x}}\right|≤1,5.[/tex] Ši funkcija taip pat yra aprėžta, kai [tex]x\to+\infty[/tex], nes kai [tex]M=1,5,\space N=2[/tex], tai su visomis [tex]x>2[/tex] reikšmėmis yra teisinga nelygybė [tex]\left|2^{\frac{1}{x}}\right|≤1,5[/tex]. Tačiau negalime teigti, jog ši funkcija yra aprėžta, kai [tex]x\to \infty[/tex], nes kai [tex]x\to 0[/tex] iš dešinės funkcija neaprėžtai didėja.

Dabar galime pagaliau susipažinti su taisykle, kuri praverčia skaičiuojant funkcijų, sudarytų iš aprėžtos ir nykstamos funkcijų sandaugos, ribas:

Jei [tex]\alpha(x)\to 0[/tex] ir funkcija [tex]f(x)[/tex] aprėžta, kai* [tex]x\to a[/tex], tai: $$\lim\limits_{x\to a}\alpha(x)\cdot f(x)=0$$*taisyklė galioja ir argumentui artėjant į begalybę.

[tex]\bullet[/tex] Įvertinkime ribą: [tex]\lim\limits_{x \to +\infty}\dfrac{\sin x}{\ln x}[/tex]:
Perrašykime ribą taip: [tex]\lim\limits_{x \to +\infty}\sin x\cdot \dfrac{1}{\ln x}[/tex]. Dabar aiškiai matome, jog funkcija yra sudaryta iš aprėžtos [tex]\sin x[/tex] ir nykstamosios funkcijos [tex]\dfrac{1}{\ln x}[/tex], kai [tex]x \to +\infty[/tex], sandaugos. Tai reiškia, kad:
$$\lim\limits_{x \to +\infty}\dfrac{\sin x}{\ln x}=0$$ [tex]\bullet[/tex] Įvertinkime ribą: [tex]\lim\limits_{x \to 0}x\cos \left(\dfrac{1}{x}\right)[/tex]:
Funkcija [tex]y=x[/tex] yra nykstamoji, o [tex]y=\cos \left(\dfrac{1}{x}\right)[/tex] aprėžta, kai [tex]x\to 0[/tex], vadinasi: $$\lim\limits_{x \to 0}x\cos \left(\dfrac{1}{x}\right)=0.$$ Tačiau tai ne vienintelis atvejis, kai nykstamosios funkcijos praverčia. Toliau pakalbėsime apie nykstamųjų funkcijų palyginimą ir ekvivalenčias nykstamąsias funkcijas:
Tarkime turime dvi nykstamąsias funkcijas [tex]\alpha(x)[/tex] ir [tex]\beta(x)[/tex], kai [tex]x\to a[/tex] (čia [tex]a[/tex] laikysime tiek baigtiniu skaičiumi, tiek begalybe). Skaičiuojant ribą [tex]\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}[/tex], galime gauti tris atvejus, kiekvienu jų mes laikysime, jog palyginome dvi nykstamąsias funkcijas ir sakysime, kad:

[tex]\bullet[/tex] Funkcija [tex]\alpha(x)[/tex] yra aukštesnės eilės negu [tex]\beta(x)[/tex] nykstamoji funkcija, jei [tex]\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}=0[/tex]
[tex]\bullet[/tex] Funkcija [tex]\alpha(x)[/tex] yra žemesnės eilės negu [tex]\beta(x)[/tex] nykstamoji funkcija, jei [tex]\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}=\infty[/tex]
[tex]\bullet[/tex] Funkcija [tex]\alpha(x)[/tex] yra tos pačios eilės kaip ir [tex]\beta(x)[/tex] nykstamoji funkcija, jei [tex]\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}=b[/tex], kur [tex]b-[/tex] baigtinis, nelygus 0 skaičius.

Palyginkime nykstamąsias funkcijas:
[tex]\bullet\space y=\sqrt{14+x}-4[/tex] ir [tex]y=\sin(x-2)[/tex], kai [tex]x\to 2[/tex]:
$$\lim\limits_{x\to 2}\dfrac{\sqrt{14+x}-4}{\sin(x-2)}=\left(\dfrac{0}{0}\right)=\lim\limits_{x\to 2}\dfrac{x-2}{(\sqrt{14+x}+4)\sin(x-2)}=\lim\limits_{x\to 2}\dfrac{1}{\frac{(\sqrt{14+x}+4)\sin(x-2)}{x-2}}=\\=\dfrac{1}{\lim\limits_{x\to 2}\frac{(\sqrt{14+x}+4)\sin(x-2)}{x-2}}=\dfrac{1}{8\lim\limits_{x\to 2}\frac{\sin(x-2)}{x-2}}=\dfrac{1}{8}$$ Nykstamosios funkcijos tos pačios eilės.

[tex]\bullet\space y=\ln x[/tex] ir [tex]y=(x-1)^3[/tex], kai [tex]x\to 1[/tex]:
$$\lim\limits_{x\to 1}\dfrac{\ln x}{(x-1)^3}=\lim\limits_{x\to 1}\dfrac{\ln x}{(x-1)(x-1)^2}=\lim\limits_{x\to 1}\dfrac{\ln x}{x-1}\cdot \dfrac{1}{(x-1)^2}=(1\cdot +\infty)=+\infty $$ Funkcija [tex]y=\ln x[/tex] yra žemesnės eilės nykstamoji funkcija, nei funkcija [tex]y=(x-1)^3[/tex].

[tex]\bullet\space y=\cos x -1[/tex] ir [tex]y=x[/tex], kai [tex]x\to 0[/tex]:
$$\lim\limits_{x\to 0}\dfrac{\cos x -1}{x}=\lim\limits_{x\to 0}\dfrac{-2\sin^2 x}{x}=-2\lim\limits_{x\to 0}\dfrac{\sin x}{x}\cdot \sin x=0$$ Funkcija [tex]y=\cos x -1[/tex] yra aukštesnės eilės nykstamoji funkcija, nei funkcija [tex]y=x[/tex].

Dabar plačiau panagrinėkime atvejį, kai dvi nykstamosios funkcijos yra tos pačios eilės.

Dvi nykstamosios funkcijos [tex]\alpha(x)[/tex] ir [tex]\beta(x)[/tex], kai [tex]x\to a[/tex] (arba [tex]x\to \infty[/tex]), bus laikomos ekvivalenčiomis, jei [tex]\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}=1[/tex] ir žymėsime: [tex]\alpha(x)\sim\beta(x)[/tex], kai [tex]x\to a\space (x\to \infty)[/tex].

Toliau pateiksime ekvivalenčių nykstamųjų funkcijų lentelę:

Žemiau pateiksime ekvivalenčių nykstamųjų funkcijų poras, čia [tex]\alpha(x)\to 0[/tex], kai [tex]x\to a[/tex] (arba [tex]x\to \infty)[/tex]:
1) [tex]\sin\alpha(x)\sim \alpha(x)[/tex]
2) [tex]\arcsin\alpha(x)\sim \alpha(x)[/tex]
3) [tex]\tan\alpha(x)\sim \alpha(x)[/tex]
4) [tex]\arctan\alpha(x)\sim \alpha(x)[/tex]
5) [tex]1-\cos\alpha(x)\sim \dfrac{1}{2}[\alpha(x)]^2[/tex]
6) [tex]\ln[1+\alpha(x)]\sim \alpha(x)[/tex]
7) [tex]a^{\alpha(x)}-1\sim \alpha(x)\cdot \ln a,\space a>0[/tex]
8) [tex][1+\alpha(x)]^p-1\sim p\cdot \alpha(x)[/tex], [tex]p∈R, p≠0[/tex]

Dabar galėsime skaičiuoti tam tikras ribas paprasčiau remdamiesi tokia taisykle:

Jei [tex]\alpha_1(x)\sim\alpha(x)[/tex], o [tex]\beta_1(x)\sim\beta(x)[/tex], kai [tex]x\to a[/tex] (arba [tex]x\to \infty)[/tex], tai teisinga lygybė:
$$\lim\limits_{x\to a}\dfrac{\alpha(x)}{\beta(x)}=\lim\limits_{x\to a}\dfrac{\alpha_1(x)}{\beta_1(x)}$$

[tex]\bullet[/tex] Apskaičiuokime ribą [tex]\lim\limits_{x\to 2}\dfrac{1-\cos(x-2)}{(x-2)\ln(x-1)}[/tex]:
$$\lim\limits_{x\to 2}\dfrac{1-\cos(x-2)}{(x-2)^2}\cdot \dfrac{x-2}{\ln(x-1)}=\dfrac{1}{2}\lim\limits_{x\to 2}\dfrac{1-\cos(x-2)}{\frac{1}{2}(x-2)^2}\cdot \lim\limits_{x\to 2}\dfrac{x-2}{\ln(x-1)}$$ Kadangi [tex]1-\cos(x-2)\sim \frac{1}{2}(x-2)^2[/tex] ir [tex]x-2\sim \ln(x-1)[/tex], kai [tex]x\to 2[/tex], tai:
$$\lim\limits_{x\to 2}\dfrac{1-\cos(x-2)}{(x-2)\ln(x-1)}=\dfrac{1}{2}\lim\limits_{x\to 2}\dfrac{1-\cos(x-2)}{\frac{1}{2}(x-2)^2}\cdot \lim\limits_{x\to 2}\dfrac{x-2}{\ln(x-1)}=\dfrac{1}{2}\cdot 1\cdot 1=\dfrac{1}{2}$$ [tex]\bullet[/tex] Apskaičiuokime ribą [tex]\lim\limits_{x\to \infty}\dfrac{2^{\frac{1}{x}}-1}{\arctan \left(\frac{1}{x}\right)}[/tex]:
Kai [tex]x\to \infty[/tex], tai [tex]2^{\frac{1}{x}}-1\sim \dfrac{1}{x}\ln 2[/tex] ir [tex]\arctan \left(\frac{1}{x}\right)\sim \dfrac{1}{x}[/tex], vadinasi:
$$\lim\limits_{x\to \infty}\dfrac{2^{\frac{1}{x}}-1}{\arctan \left(\frac{1}{x}\right)}=\lim\limits_{x\to \infty}\dfrac{\dfrac{1}{x}\ln 2}{\dfrac{1}{x}}=\ln 2$$ [tex]\bullet[/tex] Apskaičiuokime ribą [tex]\lim\limits_{x\to 0}\dfrac{\ln\cos x}{\sqrt[4]{1+x^2}-1}[/tex]:
Kai [tex]x\to 0[/tex], tai [tex]\ln\cos x\sim \cos x -1[/tex] ir [tex]\sqrt[4]{1+x^2}-1\sim \dfrac{1}{4}x^2[/tex]. Gauname:
$$\lim\limits_{x\to 0}\dfrac{\ln\cos x}{\sqrt[4]{1+x^2}-1}=\lim\limits_{x\to 0}\dfrac{\cos x -1}{\dfrac{1}{4}x^2}=-2\lim\limits_{x\to 0}\dfrac{1-\cos x}{\dfrac{1}{2}x^2}$$ Kadangi [tex]1-\cos x\sim \dfrac{1}{2}x^2[/tex], kai [tex]x\to 0[/tex], tai:
$$\lim\limits_{x\to 0}\dfrac{\ln\cos x}{\sqrt[4]{1+x^2}-1}=-2\lim\limits_{x\to 0}\dfrac{1-\cos x}{\dfrac{1}{2}x^2}=-2\cdot 1=-2$$ Dar viena galimybė pritaikyti nykstamąsias funkcijas skaičiuojant funkcijų ribas yra tokios taisyklės taikymas:

Kelių skirtingos eilės nykstamųjų funkcijų suma yra ekvivalenti žemiausios eilės dėmeniui (arba žemiausios eilės dėmenų sumai).

Nykstamosios funkcijos eilę galima nustatyti kitos nykstamosios funkcijos atžvilgiu. Tai yra daroma remiantis tokia taisykle:

Jei [tex]\alpha(x)[/tex] ir [tex]\left(\beta(x)\right)^k[/tex], [tex]k>0[/tex], kai [tex]x\to a[/tex] (arba [tex]x\to\infty[/tex]) yra tos pačios eilės nykstamosios funkcijos, tai [tex]\alpha(x)[/tex] vadinsime k-tosios eilės nykstamąja funkcija  lyginant su [tex]\beta(x)[/tex].

[tex]\bullet[/tex] Paskaičiuokime ribą: [tex]\lim\limits_{x\to 0}\dfrac{3\sin x-x^2+x^3}{\tan x+2\sin^2 x+5x^4}[/tex]
Nustatykime trupmenos skaitiklio žemiausios eilės dėmenį (ar dėmenis). Nykstamųjų funkcijų eilę nustatysime nykstamosios funkcijos [tex]y=x[/tex] atžvilgiu:
Kadangi [tex]\lim\limits_{x\to 0}\dfrac{3\sin x}{x}=3[/tex], tai [tex]3\sin x[/tex] - pirmos eilės nykstamoji funkcija lyginant su [tex]x[/tex], kai [tex]x\to 0[/tex].
Kadangi [tex]\lim\limits_{x\to 0}\dfrac{-x^2}{x^2}=-1[/tex], tai [tex]-x^2[/tex] - antros eilės nykstamoji funkcija lyginant su [tex]x[/tex], kai [tex]x\to 0[/tex].
Kadangi [tex]\lim\limits_{x\to 0}\dfrac{x^3}{x^3}=1[/tex], tai [tex]x^3[/tex] - trečios eilės nykstamoji funkcija lyginant su [tex]x[/tex], kai [tex]x\to 0[/tex].
Vadinasi [tex]3\sin x-x^2+x^3\sim 3\sin x[/tex]
Panašiai nustatome, kad [tex]\tan x+2\sin^2 x+5x^4\sim \tan x[/tex]
Vadinasi: [tex]\lim\limits_{x\to 0}\dfrac{3\sin x-x^2+x^3}{\tan x+2\sin^2 x+5x^4}=\lim\limits_{x\to 0}\dfrac{3\sin x}{\tan x}[/tex]
Dabar galime taikyti ekvivalenčias nykstamąsias funkcijas, taigi gauname:
$$\lim\limits_{x\to 0}\dfrac{3\sin x-x^2+x^3}{\tan x+2\sin^2 x+5x^4}=\lim\limits_{x\to 0}\dfrac{3\sin x}{\tan x}=3\lim\limits_{x\to 0}\dfrac{x}{x}=3\cdot 1=3$$
[tex]\bullet[/tex] Paskaičiuokime ribą: [tex]\lim\limits_{x\to 0}\dfrac{\sin 2x+\arcsin^2x-\arctan^2x}{3x}[/tex]
Lyginat su nykstamąja funkcija [tex]x[/tex], kai [tex]x\to 0[/tex], iš trupmenos skaitiklyje esančių funkcijų žemiausios eilės yra funkcija [tex]\sin 2x[/tex] (ji yra pirmos eilės, likusios dvi [tex]\arcsin^2x[/tex] ir [tex]-\arctan^2x[/tex] antros), vadinasi:
$$\lim\limits_{x\to 0}\dfrac{\sin 2x+\arcsin^2x-\arctan^2x}{3x}=\lim\limits_{x\to 0}\dfrac{\sin 2x}{3x}=\dfrac{2}{3}$$

Į šią temą įdėjau daug darbo, galėjo ir pasitaikyti klaidų, taigi nebijokite ir drąsiai komentuokite: užduokite klausimus ir pateikite pastabas. Vienpusių ribų skaičiavimą aptarsiu kitoje pamokoje.