Reikalinga pagalba kampu į horizontą mesto kūno lėkio laiko formulės išvedimui paaiškinti.

https://ibb.co/bJYg5C5

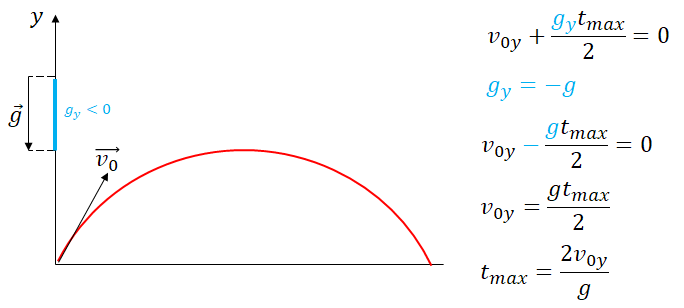
Sveiki, turbūt iš temos kyla neaiškumų, tačiau nežinau kaip dar aiškiau būtų ją pavadinti. Esu 11-tokas, pasirinkau fiziką, tačiau mane erzina vienas dalykas. Jau 9 ar 10 klasėje pastebėjau, kad išvedant fizikos formules kartais nesekami algebros reikalavimai (galbūt čia pasirodo mano matematinių žinių stoka...). Esu labiau matematikos entuziastas negu fizikos, todėl iš esmės mane logiškai trikdo tokie dalykai ir apskritai trikdo visą mano dalyko supratimą. Nuotraukoje, kurios link'ą prisegiau (tikrai ne virusas), matome kūno, kuris mestas į horizontą, lėkio formulę. Ji yra išvedama kaip matome iš viršuj dešinės formulės. Asmeniškai mėgstu pats išvesti formules, kai einu naujas temas, kad būtų aiškiau, tačiau šiuo atveju aš nesuprantu, kodėl galutinė formulė yra gaunama be minuso ženklo? Man išvedant (raudonas markeris) gaunasi, jog galutinė formulė yra su minusu. Žinom, kad laisvojo kritimo pagreičio vektorius yra žemyn, kai kūnas metamas į horizontą, todėl g=-g. Tai ar nesigautu atsakymas (lėkio laikas) su minuso ženklu, jeigu naudočiau juodo teksto galutinę formulę uždavinyje? Kartais jaučiu, jog aš kažko nežinau ar nesuvokiu išvedant šias formules, kažkokios taisyklės. Todėl ieškau pagalbos čia ir kreipiuosi į jus, fizikai, kurie galėtų paaiškinti, kodėl galutinė formulė yra be minuso ženklo, ir kaip apskritai žinoti, kada tą minuso ženklą naikinti tokiose formulėse...
Mano vienintelė prielaida, kurią padariau ties šiuo klausimu yra ta, jog jei mano gauta formulė yra su minusu, laisvojo kritimo pagreitis taip pat su minuso, tai mano galutinė formulė gaunasi su pliusu. Savaime aišku, jog gaunasi tas pats, jei -g įstatomas pačioj pradinėje formulėje. Tačiau ar tikrai juodu font'u parašytoje formulėje daroma tas pats, apie ką galvoju? Nes pradinė formulė yra su pliusu, nerodo, jog g=-g. Jeigu taip, tada tiesiog praleistas svarbus veiksmas, kurį galbūt derėtų vis dėlto parodyti mokiniams, kurie katik pradėjo šią temą...
Ačiū! Atsiprašau, jei klausimas nėra pakankamai aiškus, ar aš nesuprantu kažko elementaraus...

Esmė yra vektorių projekcijų pasirinktoje ašyje ženklai. Jeigu Oy ašį nukreipiame į viršų, tai laisvojo pagreičio vektoriaus kryptis yra priešinga šiai ašiai, todėl jo projekcija neigiama [tex]g_y=-g[/tex], perkėlus trupmeną į kitą lygybės pusę šis minusas dingsta.
Reikia suprasti, jei prie fizikinio dydžio yra indeksas y, kaip pavyzdžiui [tex]g_y[/tex], vadinasi mes kalbame apie tą dydį vaizduojančio vektoriaus projekciją pasirinktoje ašyje (pažymėta mėlyna spalva), kuri priklausomai nuo vektoriaus krypties ir pasirinktos ašies krypties gali būti teigiama arba neigiama (mūsų atveju neigiama), jei indekso nėra, vadinasi mes jau kalbame apie šio dydžio absoliutinę vertę (neneigiamą dydį). Kitaip tariant [tex]g_y[/tex] gali būti tiek teigiamas, tiek neigiamas, priklausomai nuo to, kokią pasirinktume y ašies kryptį, bet [tex]g[/tex] visada yra teigiamas apytiksliai lygus [tex]10\textrm { m/s}^2[/tex].

Dar:
Mes galime išvesti formulę, kurioje paliktume vektoriaus [tex]g[/tex] projekciją žymintį kintamąjį, tuomet gauta formulė jau būtų su minusu, kaip tavuoju atveju:
$$v_{0y}+\dfrac{g_yt_{max}}{2}=0\\\dfrac{g_yt_{max}}{2}=-v_{0y}\\g_yt_{max}=-2v_{0y}\\t_{max}=-\dfrac{2v_{0y}}{g_y}$$O tada įsistatę [tex]g_y=-g:[/tex]
$$t_{max}=-\dfrac{2v_{0y}}{-g}\\t_{max}=\dfrac{2v_{0y}}{g}$$