Užduotis iš 2019 m. Vengrijos valstybinio matematikos egzamino

Paveiksliuke duota seka, kurios nariai skaičiuojami taip:
[tex]a_{1}=1[/tex]
[tex]a_{2}=2+4+2=8[/tex]
[tex]a_{3}=3+6+9+6+3=27[/tex]
ir t.t
Įrodykite, kad sekos narys n apskaičiuojamas pagal formulę [tex]a_{n}=n^{3}[/tex]


Pagal jų egzamino vertinimą, tai uždavinys vertas 4 taškų iš 115

Dar keletas iš to pačio egzamino:

Kiek yra natūraliųjų skaičių, kurių skaitmenų suma bei sandauga yra lygi 12? (7t)

Trikampį, kurio viršūnės yra taškuose A(-6;0), B(6;0), C(0;8), kerta tiesė 3x-4y=-12. Įrodykite, kad ši tiesė dalina trikampio plotą bei perimetrą į dvi lygias dalis. (10t)

Labai gerai. Daugiau tokių  užduočių. Šaunu

Uždaviniui užtenka pagrindinės mokyklos kurso.

Štai dar viena iš to pačio egzamino, jie už ją skiria 6 taškus:

Kiek yra natūraliųjų skaičių p 1000>p , kuriems p ir 42 yra tarpusavyje pirminiai skaičiai?

Įdomu kiek Lietuvos abiturientų išspręstų šias užduotis.

Tokius uždavinius spręstų tik olimpiadininkai, kurie ruošiasi pagal olimpiadinių uždavinių programą. Vidurinės mokyklos programoje to nėra. Žemesnėse klasėse sužino kas yra pirminiai ir tarpusavyje pirminiai skaičiai ir viskas.

Na, manau, kad iš dalies mokyklinėje programoje yra viskas, ko reiktų išspręsti tokiam uždaviniui. Tereikia išskaidyti 42 pirminiais dauginamaisiais, tai bus 2*3*7 ir surasti kiek skaičių, kurie yra mažesni už 1000 dalinasi iš 2,3,7, o tai galima daryti padalinant. O olimpiadoms būtų tikrai per lengvas.

Pilnas egzaminas:

Duotas laikas: 4h
Galima surinkti 115 taškų

I dalis

1. Kvadrato ABCD kraštinės ilgis yra 4m, kvadrate įbrėžtas lygiagretainis HEFG (paveiksliukas). AH=CF=x m, BE=DG=2x m, 0<x<2.
a) Įrodykite, kad lygiagretainio plotas apskaičiuojamas pagal funkciją [tex]T(x)=4x^{2}-12x+16[/tex] (4t)
b) Raskite su kuria x reikšme lygiagretainio plotas mažiausias (4t)
c) Apskaičiuokite lygiagretainio kampų dydžius, jeigu [tex]x=1.25[/tex] (1 skaičiaus po kablelio tikslumu) (6t)


2.
a) Ketvirtas geometrinės progresijos narys yra 12, o devintas 384. Raskite pirmų šešių sekos narių aritmetinį vidurkį bei https://en.wikipedia.org/wiki/Average_absolute_deviation(nežinau kaip lietuviškai taisyklingai pasakyti) nuo vidurkio. (6t)
b) Kiek yra natūraliųjų skaičių, kurių skaitmenų suma bei sandauga yra lygi 12? (7t)

3. Išspręskite lygtis:
a) [tex](\frac{1}{3})^{2x+1}+(\frac{1}{9})^{x+1}=324[/tex] (6t)

b) [tex]\sqrt{6x-24}=\sqrt{2x-7}-1[/tex] (7t)

4.
a) Apskaičiuokite trikampės piramidės, kurios visos pagrindo kraštinės yra lygios 6cm, bei kurios kraštinė su pagrindu sudaro 30 laipsnių kampą, tūrį. (6t)
b) Ant a) dalyje minėtos piramidės užrašyti skaičiai 1,2,3,4. Išridenti skaičius 1,2,3 tikimybę yra tokia pati, o išridenti 4 ji yra penkis kartus didesnė nei išridenti 1. Apskaičiuokite kokia tikimybė, kad išmetus dvi tokias piramidės išridentų skaičių suma bus 6. (5t)

II dalis

Vienos iš šioje dalyje pateiktų užduočių mokiniai gali nedaryti

5. Iš paveikslėje pavaizduoto lapo, kurio matemnys yra 33x18 cm, iškerpamas nuspalvinta figūra ir iš jos išlankstoma dežutė.
a) Apskaičiuokite dežutės tūrį, jeigu a=7 cm (3t)
b) Raskite a,b,c reikšmes, kad dežutės tūris būtu pats didžiausias (9t)
c) Pagamintoje dežutėje pasirenkami trys taškai ir juos sujungus sudaromas trikampis. Apskaičiuokite kiek tokių trikampių yra, jeigu pasirinktos viršūnės negali būti vienoje briaunoje. (4t)


6.
a) Lygiašonio trikampio kraštinių sumos vidurkis yra 10, o standartinis nuokrypis [tex]3\sqrt{2}[/tex]. Raskite trikampio kraštinių ilgius. (6t)
b) Trikampį, kurio viršūnės yra taškuose A(-6;0), B(6;0), C(0;8), kerta tiesė 3x-4y=-12. Įrodykite, kad ši tiesė dalina trikampio plotą bei perimetrą į dvi lygias dalis. (10t)

7. Beveik visa užduotis yra apie grafų teoriją, tai jos neverčiau.

8. Žaidime reikia sudėlioti žodžius ir nuo žodžių ilgio priklauso kiek taškų gausi. Jei žodžio ilgis 1, tai 0, jei 2, tai 1, o jeigu žodžio ilgis n>=3, tai taškai skaičiuojami pagal formulę [tex]\dfrac{n^2-5n+10}{2}[/tex]
a) Ar mokinys žaisdamas gali surinkti 26 taškus? (3t)
b) Įrodykite, kad kuo ilgesnis žodis, tuo daugiau taškų mokinys gaus, bei kad jis gali gauti tik sveiką taškų skaičių. (6t)
c) Įrodykite, kad jeigu m yra natūralusis skaičius, tai mokinys žaisdamas gali surinkti [tex]2+\dfrac{m(m+1)}{2}[/tex] taškų. (7t)

9.
a) Kiek yra natūraliųjų skaičių p 1000>p , kuriems p ir 42 yra tarpusavyje pirminiai skaičiai? (6t)
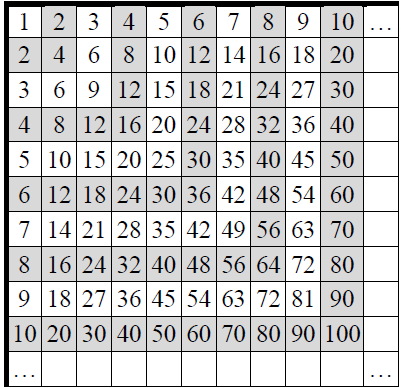
b) Paveiksliuke duota seka, kurios nariai skaičiuojami taip:
[tex]a_{1}=1[/tex]
[tex]a_{2}=2+4+2=8[/tex]
[tex]a_{3}=3+6+9+6+3=27[/tex]
ir t.t
Įrodykite, kad sekos narys n apskaičiuojamas pagal formulę [tex]a_{n}=n^{3}[/tex](4t)

c) Įrodykite, kad [tex]1^{3}+2^{3}+3^{3}+...+n^{3}=(\dfrac{n(n+1)}{2})^{2}[/tex]


Šis egzaminas yra aukštesnio lygio, kaip Lietuvoje būtų vien iš A lygio užduočių, bet Vengrijoje yra ir kitas, daug lengvesnis, kurį ir rašo dauguma mokinių. Sprendimus įkelsių po poros dienų.

[tex]8.[/tex]
[tex]a)[/tex] [tex]\frac{n^2-5n+10}{2}=26[/tex]
[tex]n^2-5n+10=52[/tex]
[tex]n_{1}=\frac{5-\sqrt{193}}{2};[/tex] [tex]n_{2}=\frac{5+\sqrt{193}}{2}[/tex]
[tex]Atsakymas:[/tex] [tex]NE[/tex]

[tex]b)[/tex] [tex][\frac{n^2-5n+10}{2}]'=n-\frac{5}{2}[/tex]
[tex]n-\frac{5}{2}=0[/tex] [tex]\rightarrow[/tex] [tex]n=\frac{5}{2}[/tex]
[tex]n∈(-∞;\frac{5}{2})[/tex] (f-ja didėja)
Žodis negali būti sudarytas iš neigiamų raidžių. Tad galime nagrinėti ši intervalą:
[tex]n∈[1;\frac{5}{2})[/tex] (f-ja mažėja)
Funkcija šiame intervale mažėja, bet sąlygoje pasakyta, kad žodis iš vienos raidės, duoda mokiniui 1 tašką, o iš dviejų - 2 taškus [tex]\rightarrow[/tex] [tex]n∈[1;\frac{5}{2}),n∈ \mathbb{N}[/tex] (f-ja didėja)
[tex]n∈(\frac{5}{2};+∞)[/tex] [(f-ja didėja)
Šiame intervale funkcija didėja. Atsižvelgiant į sąlyga galime teigti, kad:
[tex]\forall n∈[1;+∞),f(n)≤f(n+1)[/tex]

Nagrinėsime ši intervalą: [tex]n∈[3;+∞)[/tex]
, kai [tex]n=3[/tex]
[tex]n=[/tex] [tex]\frac{3^2-5 \cdot 3+10}{2}=2[/tex]
Tarkime, kad n yra sveikas skaičius ir n=k, tada n=k+1 irgi turi būti sveikasis skaičius:
[tex]\frac{(k+1)^2+5(k+1)+10}{2}=\frac{k^2-5k+10}{2}+N,N∈ \mathbb{N}[/tex]
[tex]\frac{(k+1)^2+5(k+1)+10}{2}=\frac{k^2+2k+1-5k-5+10}{2}=\frac{k^2-5k+10}{2}+\frac{2k-4}{2}[/tex]
[tex]\frac{ 2\cdot 3-4}{2}=1[/tex]
[tex]\square[/tex]
[tex]c)[/tex] [tex]2+\frac{m(m+1)}{2}[/tex]
[tex][2+\frac{m(m+1)}{2}]'=m+\frac{1}{2}[/tex]
[tex]m+\frac{1}{2}=0[/tex] [tex]\rightarrow[/tex] [tex]m=-\frac{1}{2}[/tex]
[tex]m∈(-∞;-\frac{1}{2})[/tex] (f-ja mažėja,) Šio intervalo nagrinėti nereikia, nes [tex]m∈\mathbb{N}[/tex]
[tex]m∈(-\frac{1}{2};+∞)[/tex] (f-ja didėja,) [tex]m∈\mathbb{N}[/tex] [tex]\rightarrow[/tex] [tex]m∈[1;+∞)[/tex]
[tex]m=1,[/tex] [tex]2+\frac{1(1+1)}{2}=3[/tex]
Tarkime, kad m yra sveikas skaičius ir m = k, tada m = k + 1 irgi turi būti sveikasis skaičius:
[tex]2+\frac{(k+1)^2+(k+1)}{2}=2+\frac{k(k+1)}{2}+a+1=3+\frac{k(k+1)}{2}+k[/tex]
[tex]3+\frac{3(3+1)}{2}+3=12[/tex]
[tex]\square[/tex]
Tikiuosi teisingai :/

a) Gerai

b) Gerai, bet su indukcija persistengta, galima imti tiesiog [tex]\dfrac{n^2-5n+10}{2}[/tex] ir pertvarkyti [tex]\dfrac{n(n-5)+10}{2}[/tex], 10 visada dalinsis iš 2, n ir n-5 visada bus vienas lyginis, o kitas nelyginis, tai reiškia irgi dalinsis. Taip pat būtų galima ir be išvestinių skaičiavimo, tiesiog teigiant, kad f(n+1)>f(n) ir įsistačius apskaičiavus.

c) Blogai, nes įrodai, tiesiog kad m visada bus sveikasis skaičius, o reikia įrodyti ar gali surinkti [tex]2+\dfrac{m(m+1)}{2}[/tex] taškų, o taškai skaičiuojami pagal formulę [tex]\dfrac{n^2-5n+10}{2}[/tex]