eMatematikas PRO +255
Vektorius - kryptinė atkarpa. Jei šios atkarpos galai yra [tex]A[/tex] ir [tex]B[/tex], o vektoriaus kryptis yra iš taško [tex]A[/tex] į tašką [tex]B[/tex], tai sakome, jog turime vektorių [tex]\vec{AB}[/tex] (A-vektoriaus pradžios taškas, B-pabaigos). Tą patį vektorių taip pat galima žymėti viena pasirikta mažąja raide tarkime [tex]\vec{a}[/tex].
Vektorius galima sudėti pagal trikampio, lygiagretainio arba daugiakampio taisykles:
Trikampio taisyklė
Turime du vektorius [tex]\vec{a}[/tex] ir [tex]\vec{b}[/tex]. Vektorių [tex]\vec{b}[/tex] perkeliame (tai daryti galima, nes vektorius nepasikeičia jei jį tiesiog perkeliame plokštumoje ar edvėje, nekeisdami, jo krypties ir ilgio) taip, kad jo pradžia sutaptų su vektoriaus [tex]\vec{a}[/tex] galu. Tada šių vektorių suma [tex]\vec{a}+\vec{b}[/tex] bus vektorius, kurio pradžia sutampa su vektoriaus [tex]\vec{a}[/tex] pradžia, o pabaiga su vektoriaus [tex]\vec{b}[/tex] pabaiga.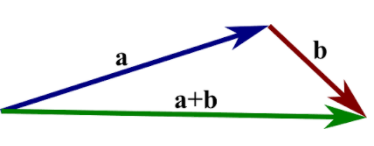
Lygiagretainio taisyklė
Vektorius [tex]\vec{a}[/tex] ir [tex]\vec{b}[/tex], kuriuos norime sudėti atidedame iš vieno taško (vėlei tą padarome keisdami vektoriaus padėtį, bet nekeisdami jo krypties ir ilgio). Laikydami, jog vektoriai yra jų ilgiams lygiose lygiagretainio kraštinėse, papildome brėžinį iki pilno lygiagretainio. Tada šių vektorių suma bus vektorius, kurio pradžia sutaps su sudedamų vektorių pradžiomis, o galas bus priešingame pradžios taškui lygiagretainio taške: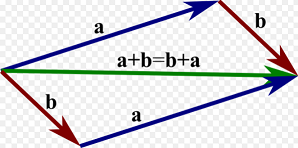
(čia galime matyti, jog lygiagretainio taisyklė praktiškai yra trikampio taisyklė, tik čia pasinaudojama vektorių lygumo apibrėžimu).
Daugiakampio taisyklė
Tai taisyklė panaši į trikampio taisyklę, tik ši taisyklė leidžia vienu metu sudėti daugiau nei du vektorius.
Norėdami sudėti kelis vektorius elgiamės taip: vektorius perkeliami taip, kad antrojo vektoriaus pradžia sutaptų su pirmojo galu, trečiojo pradžia su antrojo galu, ketvirtojo pradžia su trečiojo galu ir t.t. kol sudedami visi vektoriai. Tada šių vektorių suma bus vektorius jungiantis pirmojo vektoriaus pradžią ir paskutiniojo pridėto vektoriaus pabaigą.
pakeista prieš 1 m