Tomas PRO +4543
Įvade į funkcijų ribų skaičiavimą (šią pamoką rasite čia: http://www.ematematikas.lt/forumas/ivadas-i-funkciju-ribu-skaiciavima-t12202.html), mes paminėjome vienpusės funkcijos ribos sąvoką. Išsiaiškinome, jog funkcija turi ribą taške, jei tame taške egzistuoja abi vienpusės ribos, t.y. tiek kairinė, tiek dešininė. Dabar išmoksime paskaičiuoti šias vienpuses ribas ir remiantis jomis tirti funkcijos tolydumą taške.
Pirmiausiai susipažinkime su vienpusių ribų užrašymu.
Jei norėsime paskaičiuoti funkcijos [tex]f(x)[/tex] ribą taške [tex]x=a[/tex] iš kairės, tai rašysime: [tex]\lim\limits_{x\to a-0}f(x)[/tex]Žinodami, kaip užrašome vienpuses ribas, galime išnagrinėti pirmąjį pavyzdį, kaip yra skaičiuojamos vienpusės ribos.
Jei norėsime paskaičiuoti funkcijos [tex]f(x)[/tex] ribą taške [tex]x=a[/tex] iš dešinės, tai rašysime: [tex]\lim\limits_{x\to a+0}f(x)[/tex]
[tex]\bullet[/tex] Raskite funkcijos [tex]f(x)=\dfrac{1}{x+3^{\frac{1}{3-x}}}[/tex] vienpuses ribas, taške [tex]x_0=3[/tex]:
Nagrinėkime funkciją [tex]y=\dfrac{1}{3-x}[/tex]. Nesunku nustatyti, jog [tex]x[/tex] artėjant prie 3 iš kairės [tex]y[/tex] artėja į [tex]+\infty[/tex]. Tokiu atveju [tex]3^{\frac{1}{3-x}}[/tex] artėja taip pat prie [tex]+\infty[/tex]. Prie begalo didelio teigiamo skaičiaus pridėję 3 neišvengiamai gausime dar didesnį skaičių, taigi [tex]x+3^{\frac{1}{3-x}}\to +\infty[/tex]. Galiausiai 1 padaliję iš begalo didelio teigiamo skaičiaus gausime skaičių artimą 0, taigi galiausiai rašome: [tex]\lim\limits_{x\to3-0}\dfrac{1}{x+3^{\frac{1}{3-x}}}=0[/tex]
Kaip galėjote pastebėti vienpusių ribų skaičiavimas gan keistas ir gerokai skirtingas lyginant su funkcijos ribos taške skaičiavimu. Čia viskas paremta mums žinomų funkcijų elgsena, kurią geriausiai atspindi tų funkcijų grafikai.
Paskaičiuokime tos pačios funkcijos ribą taške [tex]x_0=3[/tex] iš dešinės.
Nagrinėdami tą pačią funkciją [tex]y=\dfrac{1}{3-x}[/tex], nustatome, jog [tex]x[/tex] reikšmėms artėjant prie 3 iš dešinės, funkcijos reikšmės artėja prie [tex]-\infty[/tex]. Tada [tex]3^{\frac{1}{3-x}}\to 0[/tex]. Kadangi šįkart gavome paprasčiausią skaičių, tai ribos skaičiavimą galime užbaigti elmentariausia aritmetika: [tex]\lim\limits_{x\to3+0}\dfrac{1}{x+3^{\frac{1}{3-x}}}=\dfrac{1}{3+0}=\dfrac{1}{3}[/tex].
Gavome, jog vienpusės ribos taške [tex]x=3[/tex] nėra lygios, taigi funkcijos riba taške [tex]x=3[/tex] neegzistuoja. Tai patvirtina ir šios funkcijos grafikas:
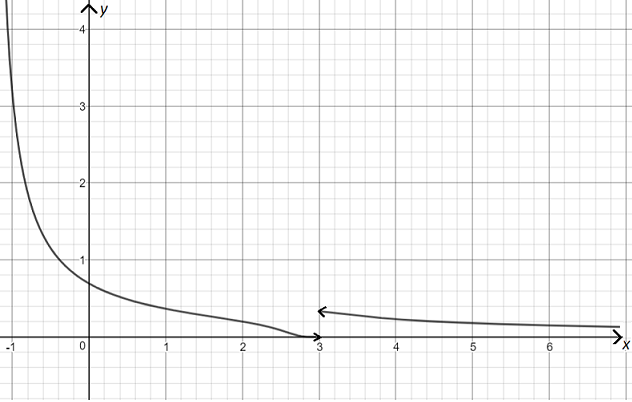
[tex]\bullet[/tex] Raskime vienpuses ribas taške [tex]x_0=2[/tex], kai funkcija duota tokia sistema:
$$f(x)=\begin{cases}x+1,\space kai\space x≤2 \\ -2x+1,\space kai\space x>2 \end{cases}$$
Kai [tex]x\to 2-0[/tex], tai [tex]f(x)=x+1[/tex], vadinasi: [tex]\lim\limits_{x\to 2-0}f(x)=\lim\limits_{x\to 2-0}(x+1)=2+1=3[/tex]
Kai [tex]x\to 2+0[/tex], tai [tex]f(x)=-2x+1[/tex], vadinasi: [tex]\lim\limits_{x\to 2+0}f(x)=\lim\limits_{x\to 2+0}(-2x+1)=-4+1=-3[/tex]
Šįkart paskaičiuoti vienpuses ribas buvo labai paprasta, kadangi funkcijos [tex]y=x+1[/tex] ir [tex]y=-2x+1[/tex] buvo apibrėžtos taške [tex]x=2[/tex]. Nubrėžkime ir šios funkcijos grafiką:

Padarę įžangą į vienpusių ribų skaičiavimą, galime aptarti trūkios funkcijos taške sąvoką:
Funkciją [tex]f(x)[/tex] vadinsime tolydžia taške [tex]a∈D_f[/tex] iš kairės, jeigu [tex]f(a)=\lim\limits_{x\to a-0}f(x)[/tex]Prisiminę neseniai nagrinėtas funkcijas, galime teigti, jog pirmoji funkcija taške [tex]x=3[/tex] nėra tolydi nei iš kairės, nei iš dešinės, nes, kai [tex]x=3[/tex] funkcija neapibrėžta, o štai antroji funkcija yra tolydi iš kairės, bet netolydi iš dešinės. Taip pat galime teigti, jog abi šios funkcijos nėra tolydžios atitinkamai taškuose [tex]x=3[/tex] ir [tex]x=2[/tex].
Funkciją [tex]f(x)[/tex] vadinsime tolydžia taške [tex]a∈D_f[/tex] iš dešinės, jeigu [tex]f(a)=\lim\limits_{x\to a+0}f(x)[/tex]
Funkciją [tex]f(x)[/tex] tolydžia taške [tex]x=a[/tex], jei ji šiame taške tolydi tiek iš kairės, tiek iš dešinės. Tai reiškia bus teisinga lygybė: [tex]f(a)=\lim\limits_{x\to a-0}f(x)=\lim\limits_{x\to a+0}f(x)[/tex].
Jei funkcija nėra tolydi taške [tex]a∈D_f[/tex], tai ji yra trūki tame taške.Trūkio taškai gali būti trijų rūšių:
Tašką [tex]x=a[/tex] vadinsime funkcijos [tex]f(x)[/tex] pirmosios rūšies trūkio tašku, jeigu jame egzistuoja abi vienpusės ribos, tačiau jos nėra lygios.Prieš tai pateiktuose pavyzdžiuose abu trūkio taškai yra pirmos rūšies. Be to esant šios rūšies trūkio taškui, galima apskaičiuoti dydį [tex]\lim\limits_{x\to a+0}f(x)-\lim\limits_{x\to a-0}f(x)[/tex], kuris vadinamas funkcijos [tex]f(x)[/tex] šuoliu taške [tex]x=a[/tex].
Tašką [tex]x=a[/tex] vadinsime funkcijos [tex]f(x)[/tex] antrosios rūšies trūkio tašku, jeigu jame bent viena vienpusė riba lygi begalybei arba neegzistuoja.
Tašką [tex]x=a[/tex] vadinsime funkcijos [tex]f(x)[/tex] pašalinamuoju trūkio tašku, jeigu šiame taške egzistuoja funkcijos riba, bet ji nėra lygi funkcijos reikšmei šiame taške arba ši reikšmė neegzistuoja.
Kadangi [tex]\lim\limits_{x\to3-0}\dfrac{1}{x+3^{\frac{1}{3-x}}}=0,\space \lim\limits_{x\to3+0}\dfrac{1}{x+3^{\frac{1}{3-x}}}=\dfrac{1}{3}[/tex], tai funkcijos [tex]f(x)=\lim\limits_{x\to3-0}\dfrac{1}{x+3^{\frac{1}{3-x}}}[/tex] šuolis taške [tex]x=3[/tex] lygus [tex]\dfrac{1}{3}-0=\dfrac{1}{3}[/tex].
Tuo tarpu antrosios funkcijos šuolis taške [tex]x=2[/tex] lygus [tex]-3-3=-6[/tex].
Žemiau pateikta funkcija [tex]f(x)=2^\frac{1}{x}[/tex]. Iš grafiko matome, jog ji yra trūki taške [tex]x=0[/tex].

Iš tiesų, jei paskaičiuosime ribą iš kairės, gausime:
Kai [tex]x\to 0-0[/tex], tai [tex]\dfrac{1}{x}\to-\infty\implies 2^\frac{1}{x}\to 0[/tex]
Jei paskaičiuosime ribą iš dešinės, gausime:
Kai [tex]x\to 0+0[/tex], tai [tex]\dfrac{1}{x}\to+\infty\implies 2^\frac{1}{x}\to +\infty[/tex]
Viena iš vienpusių ribų lygi begalybei, taigi taškas [tex]x=0[/tex] yra antros rūšies trūkio taškas.
[tex]\bullet[/tex] Paskaičiuokime funkcijos [tex]f(x)=\dfrac{x^3-1}{x-1}[/tex] vienpuses ribas taške [tex]x=1[/tex]:
Ši funkcija neapibrėžta taške [tex]x=1[/tex], tačiau galime pastebėti, jog riba šiame taške egzistuoja ir ji yra lygi:
$$\lim\limits_{x\to 1}\dfrac{x^3-1}{x-1}=\lim\limits_{x\to 1}\dfrac{(x-1)(x^2+x+1)}{x-1}=\lim\limits_{x\to 1}(x^2+x+1)=1+1+1=3$$ Taigi šiuo atveju taškas [tex]x=1[/tex] yra pašalinamasis trūkio taškas.
Trūkis vadinamas pašalinamuoju ne šiaip sau. Iš tiesų, jei mes apibrėžtume funkcijos [tex]f(x)[/tex] reikšmę trūkio taške [tex]x=a[/tex] taip: [tex]f(a)=\lim\limits_{x\to a}f(x)[/tex], tai gautume funkciją, kuri būtų tolydi šiame taške (t.y. trūkio taškas būtų pašalintas).
Žemiau pavaizdavome funkcijos [tex]f(x)=\dfrac{x^3-1}{x-1}[/tex] grafiką:

Jeigu apibrėžiame šios funkcijos reikšmę taške [tex]x=1[/tex], kaip lygią ribos reikšmei tame taške, t.y. [tex]3[/tex], tai gauname tolydžios funkcijos visuose apibrėžimo srites taškuose [tex]g(x)=x^2+x+1[/tex] grafiką, kadangi, kai [tex]x≠1[/tex], tai [tex]f(x)=x^2+x+1[/tex]. Funkcijos [tex]g(x)[/tex] grafikas bus beveik toks pats kaip ir funkcijos [tex]f(x)[/tex], skirtumas tas, jog dabar ji bus apibrėžta taške [tex]x=1[/tex] ir kartu tolydi jame.
[tex]\bullet[/tex] Išnagrinėkime tokią funkciją:
$$f(x)=\begin{cases}
\dfrac{1}{1-e^{\frac{1}{1-x}}},\space x≠0,x≠1 \\
0,\space x=0,x=1
\end{cases}$$ Raskime visus jos trūkio taškus ir nurodykime jų rūšį.
[tex]\lim\limits_{x\to 0}f(x)=\lim\limits_{x\to 0}\dfrac{1}{1-e^{\frac{1}{1-x}}}=\dfrac{1}{1-e^{\frac{1}{1-0}}}=\dfrac{1}{1-e}[/tex]
Kai [tex]f(0)=0[/tex], gauname, kad [tex]\lim\limits_{x\to 0-0}f(x)=\lim\limits_{x\to 0+0}f(x)≠f(0)[/tex], vadinasi [tex]x=0[/tex] - pašalinamasis trūkio taškas.
$$\lim\limits_{x\to 1-0}f(x)=\lim\limits_{x\to 1-0}\dfrac{1}{1-e^{\frac{1}{1-x}}}$$
Kai [tex]x\to 1-0[/tex], tai [tex]\frac{1}{1-x}\to+\infty\implies e^{\frac{1}{1-x}}\to+\infty\implies 1-e^{\frac{1}{1-x}}\to -\infty\implies \dfrac{1}{1-e^{\frac{1}{1-x}}}\to 0[/tex]
Kai [tex]x\to 1+0[/tex], tai [tex]\frac{1}{1-x}\to-\infty\implies e^{\frac{1}{1-x}}\to 0\implies 1-e^{\frac{1}{1-x}}\to 1\implies \dfrac{1}{1-e^{\frac{1}{1-x}}}\to 1[/tex]
Kadangi vienpusės ribos nelygios, tai taškas [tex]x=1[/tex] yra pirmos rūšies trūkio taškas.
[tex]\bullet[/tex] Ištirkime funkcijos [tex]f(x)=\dfrac{\cos x}{4-2^{\frac{1}{\sin x}}}[/tex] tolydumą taškuose [tex]x=0[/tex] ir [tex]x=\dfrac{\pi}{6}[/tex] ir nurodykime jų rūšį. Jei trūkio taškas bus pirmos rūšies, apskaičiuosime funkcijos šuolį tame taške.
Kai [tex]x\to 0-0[/tex], tai [tex]\dfrac{1}{\sin x}\to -\infty\implies 2^{\frac{1}{\sin x}}\to 0\implies 4-2^{\frac{1}{\sin x}}\to 4\implies \dfrac{\cos x}{4-2^{\frac{1}{\sin x}}}\to \dfrac{1}{4}[/tex]
Kai [tex]x\to 0+0[/tex], tai [tex]\dfrac{1}{\sin x}\to +\infty\implies 2^{\frac{1}{\sin x}}\to \infty\implies 4-2^{\frac{1}{\sin x}}\to -\infty\implies \dfrac{\cos x}{4-2^{\frac{1}{\sin x}}}\to 0[/tex]
Taškas [tex]x=0[/tex] yra pirmos rūšies trūkio taškas, nes vienpusės ribos šiame taške nelygios. Funkcijos šuolis šiame taške lygus: [tex]0-\dfrac{1}{4}=-\dfrac{1}{4}[/tex].
Tiriame tolydumą taške [tex]x=\dfrac{\pi}{6}[/tex] (šįkart atidžiau žiūrėsime iš kurios pusės artėjama prie tam tikros reikšmės):
Kai [tex]x\to \frac{\pi}{6}-0[/tex], tai [tex]\dfrac{1}{\sin x}\to 2+0\implies 2^{\frac{1}{\sin x}}\to 4+0\implies 4-2^{\frac{1}{\sin x}}\to 0-0\implies \dfrac{\cos x}{4-2^{\frac{1}{\sin x}}}\to -\infty[/tex]
Kai [tex]x\to \frac{\pi}{6}+0[/tex], tai [tex]\dfrac{1}{\sin x}\to 2-0\implies 2^{\frac{1}{\sin x}}\to 4-0\implies 4-2^{\frac{1}{\sin x}}\to 0+0\implies \dfrac{\cos x}{4-2^{\frac{1}{\sin x}}}\to +\infty[/tex]
Kai bent viena funkcijos vienpusė riba taške yra begalybė, tai tas taškas yra antrosios rūšies trūkio taškas. Toks yra taškas [tex]x=\frac{\pi}{6}[/tex].
pakeista prieš 4 m