Tomas PRO +4543
Danieliuss5, taip atsakymas 5, kažkaip nebemoku teisingai dvinario kvadrato rasti.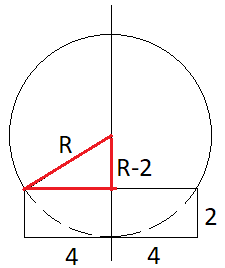
Gaunasi tokia lygtis:
[tex]4^2+(R-2)^2=R^2[/tex]
Jei kam neaišku dėl paveikslėlio rašykit.
Forumas
Matematikos PUPP užduotis 2018
Tomas PRO +4543
O ką pats tu gauni skaičiuodamas? Nes mano skaičiavimais tas Wolfram'as (aukštosios matematikos studentų išsigelbėjimas) čia nesąmones tokiu atveju rodo.
Danieliuss5 +5
Karoli,
pas jus įvelta klaida, atsakymas 11.3 yra ne n ≥ 17, o n ≥ 27, jeigu įsistatysite 17, tai pamatysite. Spėju, kad tiesiog parašėte blogą skaičių, nes nelygybė klaidų neturi.
pakeista prieš 5 m
Tomas PRO +4543
R = 5 cm pagal tavo brėžinį ir lygtį.Taip, Karoli, jau minėjau, kad netikėtų problemų turėjau su dvinario kvadratu.
Tomas PRO +4543
Galbūt aš ką nors praleidau. Su kokiomis konkrečiau problemomis susidūrei?Problema buvo ne ta, kad sėdėjau ir galvojau, kaip tą dvinarį pakelti kvadratu, o tiesiog netikėtai gavosi, jog ne taip pritaikiau formulę ir tiek. Aplamai ir tą uždavinį su rutuliu irgi neiškart išsprendžiau, čia manau toks šaltas dušas turėjo būti dešimtokams, nes pats dėžės ir rutulio uždavinys nenaujiena, bet čia jis kiek įdomiau pateiktas. Uždavinys tikrai nesudėtingas, kai viską permąstai, bet yra ką paveikti.
Tomas PRO +4543
O tai jis tau atrodo neadekvatus? Per sudėtingas?
Tomas PRO +4543
Karoli, manau užduotis vertini neįsijausdamas į pačio dešimtoko galimybes. Kad tokia užduotis buvo yra gerai ir tai yra sveikintina, bet tikrai nereikia, jog tai taptų dominuojančiais uždaviniais. PUPP neprivalo tikrinti vien tik aukštesnio lygio matematines žinias. Tam, kad žmogus galėtų save vadinti baigusiu pagrindinės matematikos kursą tikrai pakanka, jog jis nors mokėtų nuėjęs į parduotuvę pasiskaičiuoti procentus ir mokėtų pritaikyti, kad ir tas juokingai mums atrodančias stačiakampio ploto formules. VBE jau kitas dalykas, ypač, kai jis nėra privalomas. Čia jau turi būti tikrinamos žinios rimtai, nes žmonės vėliau stoja į universitetus, o ten jau kitas lygis ir reikia, kad žmogus parodytų galintis tą lygį priimti.
Tomas PRO +4543
Aš tik sutikčiau, jog NEC nepasistengė patikrinti visų per 10 metų sukauptų žinių. Panašu, jog buvo nueita keliu: prikrausim standartinių, nesudėtingų uždavinių ir kad nebūtų vėl peikiami dėl per lengvų egzaminų, įmesim kokį vieną kitą sudėtingesnį. Nors mano nuomone, geriau tie uždaviniai visi būtų buvę maždaug vidutinio sunkumo, bet būtų patikrintos žinios plačiau, ar bent jau kvadratinę lygtį būtų paprašę išspręsti. Aišku turime atkreipti dėmesį, jog patikrinimui skiriama ne tiek jau ir daug laiko.
Tomas PRO +4543
Žmogus, baigęs 10 metų mokyklą, turėtų sugebėti mąstyti t.y. ne tik nuolaidas skaičiuoti, bet ir mąstyti abstrakčiai.Dėl to tokių uždavinių, kurie tikrintų abstraktų mąstymą reikia, bet jei mes prikrausime patikrinimą vien tik tokiais uždaviniais ar vėliau bus normalu matyti minias pasipiktinusių dešimtokų, kurie pajėgūs išspręsti lengvesnius uždavinius, bet patikrinimas jiems nesuteikė galimybės to parodyti.
Prisiminkime nuo ko prasidėjo matematika: nuo taikymų. Taigi pabaigę 10 metų matematikos kursą mokiniai turėtų parodyti, jog gyvenime sugebės dažniausiai pasitaikančiose situacijose pritaikyti matematines žinias, nes tikrai didžiajai daliai jų tas rutulio dėžėje klausimas bus sprendžiamas pirmą ir paskutinį kartą, o į parduotuvę procentų paskaičiuoti eisime visi neišvengiamai ir jei to nemokėsime, turėsime gėdingai to prašyti daryti kitų arba siųstis kokią išmanią programėlę.
Tomas PRO +4543
Aš problemą ir matyčiau tame, jog mes neskirstome mokinių pagal gebėjimus, o tai reiktų daryti kiek galima anksčiau. Tebūnie būtų pajėgių ir norinčių mokytis mokinių grupė, tada jiems galima duoti ir sudėtingesnį patikrinimą, bet kol kas kol visi mokosi vienoje krūvoje turime būti teisingi visų pusių atžvilgiu, galime kalbėti tik apie procentinę dalį, tų sudėtingesnių uždavinių, bet ji tikrai neturėtų būti nusverta vien tik į gabių mokinių pusę.
Nori sudalyvauti šioje temoje ir parašyti savo pranešimą? Prisijungti »